Colarinho - Outro Modelo

Para fins didáticos farei a demonstração do cálculo do colarinho em um novo modelo, devo lembrar que esta publicação é para fins didáticos ou seja para entendermos como é feito o colarinho em outros países como nos EUA e também tenho visto em diversas fotos de obras nos outros países da América do Sul.

Aqui no Brasil somos regidos pela norma NBR 9062, em que este modelo não é adotado.

Farei um breve comentário no final deste exemplo, este exemplo tem como parâmetros geométricos e de carga que foram calculados para uma obra de Manaus com Colarinho Liso.   

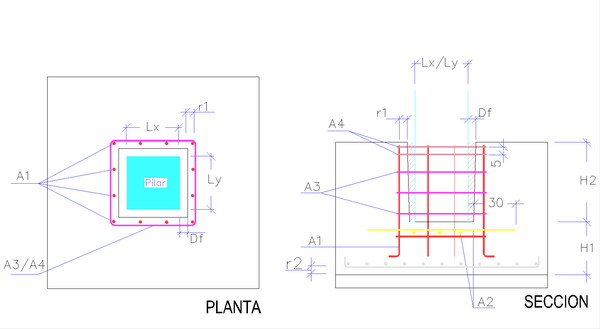
Vejamos na figura abaixo como é a distribuição de forças no colarinho neste modelo de cálculo

Demonstração da formulação:

Momento no ponto "A" da figura acima:

M + N(a/2) + HD  * 0.90h = HB * 0.80h +  μ HB * a + R(a/2+a/6)   

Reação na base da coluna:

R= N - μ HB

Substituindo R na expressão temos:

HB = (M - 0.17aN + 0.90hHD) / ((0.8h +  μ 0.33 a)

Fazendo aproximação de que h=0.9*1.5a e que para interface LISAS   μ = 0.30 a equação fica bem simplificada para Colarinhos Lisos:

HB = 1.14M/h - 0.15N + 1.03HD

Vamos ao exemplo:

Geometria do pilar:

hpil	m	0.800
bpil	m	0.400

a) Cálculo do embutimento:

h= 1.5*0.80 = 1,20m

Calculemos o comprimento de ancoragem por sua norma para verificar se este comprimento atende:

fb = 0.50*Raiz(Fck)= 0.50* Raiz (30) = 2.74 Mpa

 Como o pilar é com ferros 12 ferros de 20mm (37.70cm2) teremos para ancoragem:

Lp= (0.87*Fyd*As) / (Fb * Pi D) = (0.87* 500/1.15*37.70)  / ( 2.74*3.14*2) => 83cm 

Então temos o comprimento de embutimento:

h=   83   + 0.1h + cobrimento = 83+0.1*80+3= 94cm logo 120cm predomina sobre a ancoragem 

b) Espessura da parede hc

hc= 0.18*b + 0.07 = 0.18*0.40 + 0.07 = 0.142m => adota-se 15cm

c) Forças no colarinho:

HB = 1.14M/h - 0.15N + 1.03HD

Solicitações do Pilar que estamos estudando:

Nd	tf	52.20
Md	tf.m	19.40
Vd	tf	0.30

Logo temos substituindo os valores:

HB = 109.09 KN

HA = HB - VD = 106.09 KN

d) Armações 

São as seguintes disposições das armaduras

Temos então para o aço CA50A:

AsB= HB / (0.87*Fyd) = 109.09 / (0.87*500/1.15) = 2.88cm2   pode ser 4 ferros 10mm

Asa= (HA - μ*R ) / (0.87*Fyd)   

sendo: 

μ = 0.30

R= N- μ * HD = 521.10 KN

esta armadura fica negativa então se utiliza a mesma do bordo superior 2.88cm2 

Momento para cálculo da armadura vertical:

Mv= M + HD * h = 194.36 KN

braço de alavanca Z= H pilar + folga (5cm *duas vezes) + espessura parede/2=

Z= 0.80 + 0.10 + 0.15/2 = 0.975m

Logo:

Asv= Mv / (0.87*Fyd*Z)= 5.27cm2 

Esta armadura vertical é feita em laço, ou seja com duas pernas, se adotando ferros de 10mm teriamos 8pernas x 0.78cm2 = 6.28cm2. Estes ferros são posicionados ema cada eixo da parede. 

Como o pilar sofre um momento em HA e HB devemos reforçar a armadura do pé do pilar com estribos e ferros em "U"

Estribos: Hbst= 0.11N= 5.74KN e temos Abst=5.74/(0.87*250)= 0.26cm2 colocados no comprimento do embutimento.O estribo adotado supera esta ferragem e seu valor é bem pequeno.

Reforço em"U": As= HA /(0.87Fyd) = 106.09/ (0.87*500/1.15)= 2.80cm2 ou seja 4 ferros 10mm

e) Verificação da  pressão de contato:

Fc= N/area contato= 52.200/(40*80) = 16.31Kg/cm2

este valor é corrigido dividindo-se por 0.60 Fc corr= 16.31/0.60 = 27.18Kg/cm2 = 2.71Mpa<30<Mpa adotados para o concreto da fundação.

COMENTÁRIOS:

Como vimos as tensões no concreto não são calculadas, o calculo é bastante simples e as armaduras são bem menores. Mas estas tensões formadas pela alavanca de HA e HB podem originar problemas como a fissuração no concreto, nada como se fazer ensaios. Mas deve-se ter ensaios que foram realizados com este tipo de colarinho, mas não possuo.

Como conclusão sei que este modelo  é muito fácil de se produzir em obras e seu custo é baixo, mas é preciso estudos de confirmação em laboratório.

Eng Ruy Serafim de Teixeira Guerra

Abaixo imagens deste colarinho: